| Textes, croquis et photos (sauf mention contraire) Claude Beaudevin (1928 - 2021) | PrÃĐsentation et mise en page Bruno Pisano |
|
|
| TracÃĐ thÃĐorique de la surface d'une masse de glace en ÃĐcoulement |
 |
 |
 |
| Ãcrit par Claude Beaudevin | |||||||
| Samedi, 27 Mars 2010 21:40 | |||||||
Le traitement mathÃĐmatique thÃĐorique de la questionOn sait que, en rÃĐgime ÃĐtabli, l'altitude de la surface d'une masse de glace de largeur infinie, libre de se mouvoir sur une pente, est donnÃĐe par la formule de Nye-Lliboutry [L. Lliboutry, 1975], dÃĐmontrÃĐe à partir des propriÃĐtÃĐs physiques de la glace (nous l'appellerons dans tout ce qui suit : la formule) : 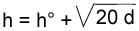 oÃđ :
h = altitude de la glace (en mÃĻtres) en un point situÃĐ Ã une distance d (en mÃĻtres) du front de la masse de glace, h° = altitude de ce front. Cette formule est valable ÃĐgalement pour les glaciers de vallÃĐe "en premiÃĻre approximation" [Monjuvent, 1978]. Est-il possible de prÃĐciser cette affirmation ? C'est ce que nous nous proposons de faire dans cette page.
Les rÃĐsultats obtenus pour les diffÃĐrentes vallÃĐes ÃĐtudiÃĐes, que l'on pourra examiner dans les pages correspondantes, montrent frÃĐquemment un bon accord entre la formule et la position des sites caractÃĐristiques dans les parties moyennes et basses des vallÃĐes alpines. On consultera en particulier le graphique relatif à la vallÃĐe de Certains pourront toutefois s'ÃĐtonner que la surface d'un glacier puisse Être ramenÃĐe à une formule mathÃĐmatique, simple de surcroÃŪt et dans laquelle le modelÃĐ du terrain sous-jacent n'intervient pas. L'examen des glaciers actuels peut effectivement en faire douter. Mais n'oublions pas que les glaciers que nous avons actuellement sous les yeux diffÃĻrent des grands appareils quaternaires par leur taille, beaucoup plus modeste (à l'exception toutefois des grandes calottes telles que celles du Groenland et de l'Antarctique). Si les formes des glaciers actuels sont sensiblement les mÊmes que celles des grands appareils quaternaires, ainsi que nous l'avons vu à la page sur les diffÃĐrents types de glaciers, de nombreuses diffÃĐrences apparaissent toutefois lorsqu'on les examine dans le dÃĐtail. Qui, à l'examen d'un paysage au crÃĐpuscule, pourrait avoir idÃĐe de la splendeur du plein soleil ? Au risque de choquer certains, disons qu'il existe la mÊme diffÃĐrence entre les gigantesques fleuves de glace du quaternaire et nos glaciers maigrichons actuels qu'entre une belle pomme, pleine, luisante... et le trognon qui en marque la fin.
Les appareils actuels, avec leurs faibles dimensions, sont sensibles aux irrÃĐgularitÃĐs du fond des vallÃĐes et aux variations de leur largeur, qu'ils traduisent par des ruptures de pente et des chutes de sÃĐracs. Jean Giono dirait que sous leur peau, on devine les os de la montagne. Les grands glaciers quaternaires des Alpes prÃĐsentaient, quant à eux, des ÃĐpaisseurs qui pouvaient atteindre 1.000 m, voire mÊme 2.000 m au-dessus des ombilics et leur largeur atteignait parfois 30 km. C'est ainsi que du col des Aravis jusqu'aux contreforts du Mont Blanc s'ÃĐtendait une "mer de Glace" large de 25 km. De mÊme au-dessus de Gap. La surface des glaciers pouvait donc suivre d'assez prÃĻs la formule thÃĐorique qui traduit l'indiffÃĐrence quasiment parfaite des grands appareils quaternaires aux irrÃĐgularitÃĐs de leurs lits. Le domaine de validitÃĐ de la formule de Nye-LliboutryComme la plupart des formules, celle-ci possÃĻde un domaine de validitÃĐ dont il convient, avant toute chose, de bien prÃĐciser les limites. Reprenons donc les termes de l'ÃĐnoncÃĐ qui prÃĐcÃĻde.
Il convient donc de tenir compte de ces divers ÂŦ effets Âŧ, que nous allons maintenant dÃĐtailler.
L'effet de paroiLe premier effet, le plus rÃĐpandu â et qui nous intÃĐressera au premier chef dans le cadre de cette ÃĐtude â se rencontre essentiellement dans les parties hautes des vallÃĐes. ConsidÃĐrons par exemple la Romanche. Au-dessus du Bourg d'Oisans (IsÃĻre), la formule indique une altitude de la surface du glacier wÞrmien ÃĐgale à 1.500 m, alors que des dÃĐpÃīts morainiques de cette ÃĐpoque peuvent Être observÃĐs jusqu'à 1.760 m au-dessus du Bourg, sur l'arÊte joignant le col du Solude à PrÃĐgentil. Ces dÃĐpÃīts renferment de nombreux ÃĐlÃĐments cristallins, alors que le bassin versant de Villard-Reymond n'est formÃĐ que de terrains sÃĐdimentaires ; ils n'ont donc pu Être dÃĐposÃĐs ici que par le glacier de la Romanche [carte gÃĐologique au 1/50 000 Vizille]. Cette constatation est gÃĐnÃĐrale : dans le haut des vallÃĐes, les glaciers ont atteint des altitudes supÃĐrieures à celles que la formule permet de calculer. Pourquoi la formule, qui donne de bons rÃĐsultats dans le bas des vallÃĐes, cesse-t-elle de le faire plus en amont ? Lorsqu'on examine la surface de glaciers de vallÃĐe actuels des Alpes ou de l'Himalaya, on constate que celle-ci peut prÃĐsenter trois types de modelÃĐ :
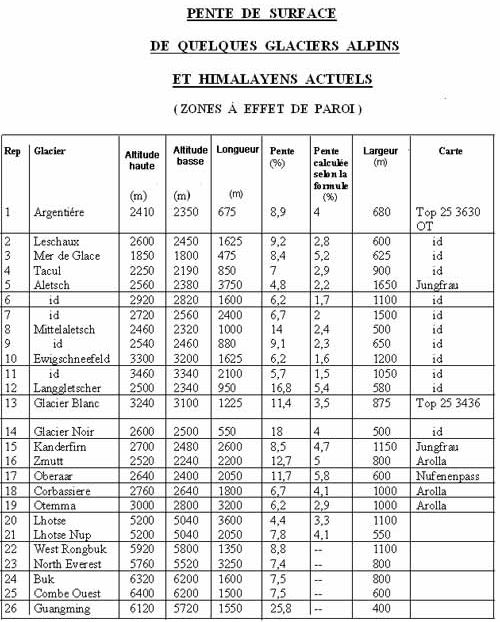
Le tableau suivant donne, pour un certain nombre de zones de ce dernier type appartenant à des glaciers français et suisses ainsi qu'à quelques appareils himalayens, la valeur de la pente en fonction de la largeur de la vallÃĐe.
La pente est celle des zones à effet de paroi. La largeur est mesurÃĐe au niveau de la surface du glacier.
Les rÃĐsultats sont regroupÃĐs sur le graphique ci-dessous. Les points en noir correspondent aux glaciers alpins, ceux en rouge aux glaciers himalayens. 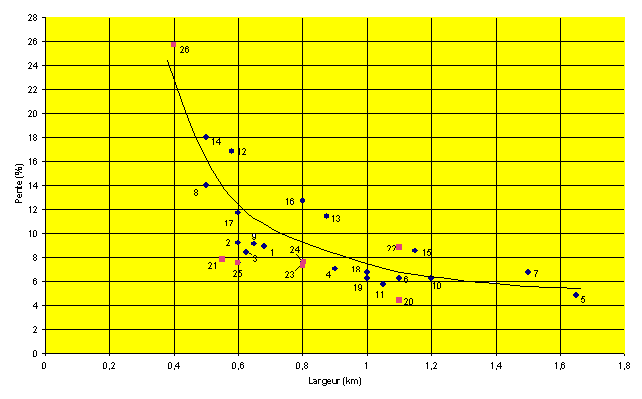 En dÃĐpit d'une forte dispersion â due en particulier au fait que sa seule largeur ne suffit pas à caractÃĐriser une vallÃĐe â il apparaÃŪt que la pente est d'autant plus faible que la vallÃĐe est plus large. Ce rÃĐsultat n'a rien de surprenant. En effet le mouvement d'un glacier rÃĐsulte de l'action de deux forces antagonistes :
Plus les dimensions de l'auge sont importantes, plus faible est l'influence du frottement sur le mouvement du glacier. à la limite, pour une largeur trÃĻs grande, on retrouverait les rÃĐsultats donnÃĐs par la formule. Inversement, plus la vallÃĐe est ÃĐtroite, plus les frottements sont importants et plus la pente du glacier doit Être grande pour les vaincre. Cet effet de paroi, classique en mÃĐcanique des fluides, est le premier de ceux que nous annoncions en tÊte de page et qui viennent altÃĐrer la belle simplicitÃĐ de la formule. Mais comprenons nous bien : sa largeur n'est, bien entendu, pas le seul facteur qui caractÃĐrise la forme d'une vallÃĐe et donc les pertes de charges que subit le glacier qui la parcourt. C'est seulement le paramÃĻtre le plus facile à utiliser et le seul d'ailleurs dont on dispose dans la majoritÃĐ des cas. La vallÃĐe du RhÃīne, entre Martigny et LÃĐman, peut constituer un cas d'ÃĐcole. Le tableau ci-dessus montre que le glacier actuel le plus large (1,65 km), prÃĐsentant la pente la plus faible, est celui d'Aletsch (RepÃĻre 5). Ceci peut Être mis en relation avec le fait que la vitesse maximale de ce glacier, vers la sortie de Concordiaplatz, est comparable à celle des deux glaciers groenlandais les plus rapides du monde [Les Glaciers, AmÃĐdÃĐe Zryd, ÃĐditions Pillet, 2001]. De l'ensemble des graphiques figurant sur ces pages, on peut dÃĐduire que, sous rÃĐserve des paragraphes qui vont suivre, la formule rend bien compte de l'altitude atteinte par la glace dans le bas des vallÃĐes, tant que la largeur du glacier au niveau supÃĐrieur de la glace restait supÃĐrieure aux valeurs figurant sur le graphique ci-dessus. C'ÃĐtait le cas dans le bas des vallÃĐes alpines, puisque l'on relÃĻve les largeurs suivantes :
La meilleure dÃĐmonstration de l'exactitude de la formule nous paraÃŪt Être constituÃĐe par ce dernier glacier.
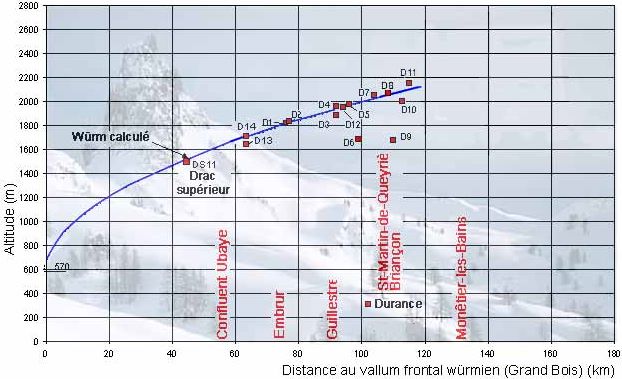
Il convient de garder à l'esprit que la courbe doit Être considÃĐrÃĐe comme joignant entre eux les points reprÃĐsentatifs des sites caractÃĐristiques les plus ÃĐlevÃĐs â c'est leur enveloppe, au sens mathÃĐmatique du mot â et non comme une moyenne entre tous les points figurant sur le graphique. On voit alors que, de Sisteron jusqu'au premier rÃĐtrÃĐcissement à moins de 4 km, qui se situe 108 km en amont, à Saint-Martin-de-QueyriÃĻres, tous les points se placent trÃĻs correctement par rapport à la courbe. Il en est de mÊme pour le glacier de l'IsÃĻre (voir à ce sujet la page sur l'altitude atteinte par le glacier de l'IsÃĻre) oÃđ l'on remarque que les points reprÃĐsentatifs des sites I1, I2, I3 et I4 se placent parfaitement sur la courbe. Les effets de paroi dans la Cluse de Voreppe, large de 4 km ÃĐtaient donc nÃĐgligeables. Selon les approximations faites dans le calcul de la formule, on peut hÃĐsiter entre des valeurs de coefficient ÃĐgales à 20 ou à 23. L'application faite ci-dessus au glacier de la Durance montre que le coefficient 20 est bien celui qu'il convient d'utiliser dans la formule.
L'effet de lobe ou effet d'ÃĐtalementLe second cas oÃđ la formule ne rend pas exactement compte de la rÃĐalitÃĐ se rencontre dans les lobes qui terminent, dans les plaines de piÃĐmont, certains glaciers alpins et alaskiens et dont on trouvera un exemple actuel remarquable à la page sur le glacier Malaspina. C'ÃĐtait le cas de celui du glacier wÞrmien du RhÃīne, par exemple, dont le lobe terminal s'ÃĐtalait en patte de lion (ou en patte d'ours ou en pecten, l'animal dÃĐpendant de l'auteur) sur le plateau molassique suisse ainsi que sur la plaine, ÃĐgalement molassique, de La Tour du Pin. à Martigny, par exemple, la surface du glacier ne se trouvait qu'à 1.750 m [Labhart et Decrouez, 1997] â ou vers 2.000 m, ainsi que semblent le montrer des ÃĐtudes plus rÃĐcentes â et non à 2.300 m comme l'indique la formule. Nous l'avons dit plus haut, la cause de cette divergence doit Être recherchÃĐe dans le tracÃĐ des lignes de courant qui divergent, dans le cas de tels lobes de piÃĐmont, alors qu'elles sont parallÃĻles dans celui d'une masse de glace de largeur infinie (ou constante), cas d'ÃĐcole ayant servi à l'ÃĐtablissement de la formule.
On trouvera des exemples, parfois trÃĻs esthÃĐtiques :
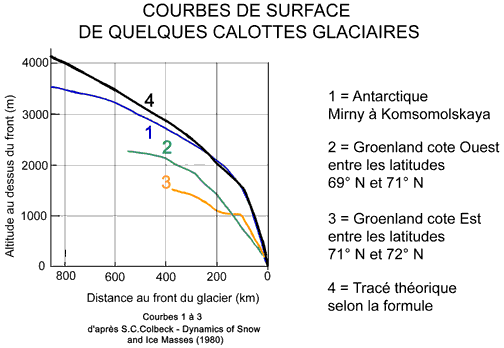
L'effet d'ÃĐtalement est maximum dans le cas des grandes calottes glaciaires. Les courbes ci-dessous permettent de comparer les tracÃĐs des surface de quelques calottes (Antarctique, Groenland) aux valeurs fournies par application de la formule.
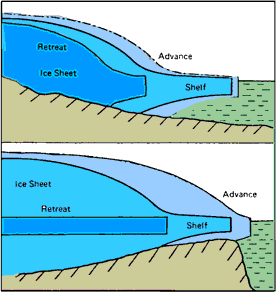
On constate que celle-ci conduit toujours à des altitudes ÃĐgales ou supÃĐrieures à celles de la rÃĐalitÃĐ. Dans le cas de l'Antarctique, la formule reprÃĐsente bien la rÃĐalitÃĐ jusqu'à 300 km environ du front du glacier; plus en amont, la surface rÃĐelle se tient toujours en dessous de la valeur calculÃĐe. Ceci n'a, a priori, rien de surprenant, puisque la formule est ÃĐtablie dans le cas de lignes de courant parallÃĻles â cas d'un glacier de largeur infinie ou constante â alors que celles des glaciers de calotte divergent à partir des points culminants. Les lobes glaciaires font l'objet d'une page spÃĐciale sur les glaciers du Spitzberg, d'Islande et de l'Alaska. L'effet de langueMÊme en l'absence de lobe, le calcul conduit, pour la partie terminale d'une langue glaciaire, à des rÃĐsultats qui diffÃĐrent de la rÃĐalitÃĐ. Selon la formule, en effet, les derniers mÃĻtres du parcours du glacier devraient se prÃĐsenter sous la forme d'une surface de glace verticale ; en fait, la pente des langues frontale est plus faible, ainsi que peuvent en tÃĐmoigner tous ceux qui les ont parcourues, crampons aux pieds. Ceci nous paraÃŪt imputable à l'importance que prennent alors les termes secondaires. A remarquer que cette pente est plus soutenue pendant les phases d'avancÃĐe du glacier qu'au cours des pÃĐriodes de stagnation ou de dÃĐcrue. L'effet de flottaisonPour Être complet, nous mentionnerons un dernier effet, bien qu'il ne se rencontre pas dans les Alpes : lorsqu'un glacier se termine dans l'ocÃĐan â cas que l'on rencontre au Spitzberg, en Alaska et en Argentine â les derniÃĻres longueurs du glacier sont soulevÃĐes par la poussÃĐe d'ArchimÃĻde. Elles flottent et leur pente devient trÃĻs faible. Il s'agit d'un glacier "vÊlant" (calving glacier), qui vÊle des icebergs. Le glacier plonge alors dans l'ocÃĐan par une falaise verticale de quelques dizaines de mÃĻtres de hauteur... et on n'oubliera pas que sa hauteur sous l'eau est encore bien plus grande. La formule ne s'applique donc pas ici !
Stricto sensu, cet effet de flottaison dans un ocÃĐan ne s'est pas produit dans les Alpes au cours des glaciations quaternaires. Mais il n'est pas exclu qu'à dÃĐfaut d'ocÃĐan, des lacs suffisamment profonds aient pu jouer le mÊme rÃīle, tels les grands lacs qui, en fin de glaciations, sont apparus dans les vallÃĐes. Voir à ce sujet la page sur les grands lacs quaternaires. Ces glaciers "vÊlants" se comportent diffÃĐremment des autres glaciers en ce qui concerne la sensibilitÃĐ aux variations du climat, ils peuvent Être en crue alors que les autres appareils sont en dÃĐcrue. Voir à ce sujet la page les glaciers vÊlants. Signalons enfin â sans aucune application aux glaciers alpins, bien entendu â que la surface d'un glacier est parfaitement horizontale lorsque celui-ci "flotte" sur un lac sous-glaciaire de grandes dimensions. C'est le cas de la calotte antarctique dans les environs de la station de Vostok, oÃđ elle repose sur l'immense lac homonyme (250 x 50 km). ConclusionLes lignes qui prÃĐcÃĻdent nous permettent à prÃĐsent de conclure. La formule de Nye-Lliboutry s'applique trÃĻs convenablement aux glaciers de vallÃĐes tant que la largeur de ceux-ci au niveau supÃĐrieur de la glace est suffisante, supÃĐrieure, pour donner un ordre de grandeur, à 4 km. Elle ne peut Être utilisÃĐe, par contre, ni pour une calotte glaciaire, ni dans le cas de glaciers de piÃĐmont prÃĐsentant un lobe trÃĻs ÃĐtalÃĐ ni dans les derniÃĻres longueurs d'une langue glaciaire. Enfin, notons que la surface d'un glacier n'obÃĐit à la formule que si sa langue terminale est libre de fixer sa position et son altitude, ce qui est le cas d'un appareil pouvant circuler librement dans une vallÃĐe suffisamment large et descendante. Si, par contre, il rejoint un autre glacier qui lui impose son altitude terminale ou s'il remonte une vallÃĐe "ascendante", la formule ne convient pas. Ceci s'applique tout particuliÃĻrement aux diffluences, par exemple à celle du glacier rissien de la Durance au-dessus du Seuil Bayard.
Que se passe-t-il à la confluence de deux glaciers ? Cliquez ici pour le savoir. |
|||||||
| Mise à jour le Lundi, 24 Octobre 2016 07:13 |


 Certains mots à la signification spÃĐcifique sont ÃĐcrits en bleu et soulignÃĐs en pointillÃĐs. Si vous laissez la souris dessus, une info-bulle affichera leur dÃĐfinition.
Certains mots à la signification spÃĐcifique sont ÃĐcrits en bleu et soulignÃĐs en pointillÃĐs. Si vous laissez la souris dessus, une info-bulle affichera leur dÃĐfinition.